![next]()
![up]()
![previous]()
Next:
About this document ...
Circular Polarization States for Light,
and quarter-wave
Plates
We may describe a monochromatic, plane polarized light wave by its electric
field vector:
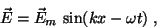 |
(1) |
where 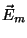 is the amplitude. Given that the wave moves with
speed
is the amplitude. Given that the wave moves with
speed 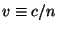 , with n the index of refraction of
the material through which it moves, the (single) color of the light is
determined by any of various different parameters that we traditionally use to
describe it:
, with n the index of refraction of
the material through which it moves, the (single) color of the light is
determined by any of various different parameters that we traditionally use to
describe it:
 |
(2) |
Note also that when the light wave is travelling through some material,
with the index of refraction different from 1, then the frequencies are
unchanged, while the wavelength and wavenumber do change.
Various polarization states of the wave
are characterized by the way the amplitude vector for the electric field depends
on time:
- When
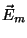 is constant in time, it always points in the
same direction; we refer to this case as plane polarization.
is constant in time, it always points in the
same direction; we refer to this case as plane polarization.
- When the magnitude,
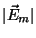 is constant, but the direction rotates with
time, we refer to that as circular polarization.
is constant, but the direction rotates with
time, we refer to that as circular polarization.
- When not even the magnitude is constant, we refer to that as elliptical
polarization.
The elliptical case is clearly the most general
case; however, it is more complicated than we need to consider here.
Furthermore, your text does a reasonable job of describing the details of plane
polarized light. Therefore, the purpose of these extra notes is to consider the
case of circular polarization. In principle there are two sorts of circular
polarization; the one where the electric vector rotates to the right and the one
where it rotates to the left, referred to as left-circular and right-circular
polarizations. However, while it is definitely true that there are these two
kinds (or possibilities), there is considerable disagreement about how one
labels which one is which; therefore, we will not do so, but simply refer to
both as circularly-polarized light, remembering, occasionally, that there are
indeed two kinds. It is true that individual photons created by a single,
individual atom always has an electric field that is circularly polarized.
However, this is an uncommon way to be looking at light waves, since these waves
usually involve very many photons--trillions at the very least--so that the
polarization state of any light wave we are observing will be some sort of an
average over very many differently-oriented states of the individual photons;
therefore, it is usually expected that any incoming light wave is
unpolarized unless something has been done to it to select that state in
a certain way.
We want now to spend a little time
discussing methods to select the polarization state of an outgoing light wave.
Plane Polarization by Using Polarizers
As we know from the textbook, there are particular materials, known as
polarizers, that selectively absorb light that has its electric field in
a certain direction, while passing light directly on when its electric field is
polarized in the perpendicular direction. This perpendicular direction your
textbook refers to as the polarizing direction, or axis. When a light
wave strikes a polarizer with an electric field vector that is in neither of
these two (perpendicular) directions, we can easily visualize what happens by
making a standard vector decomposition of that electric field into its
components relative to a basis for (2-dimensional) vectors that is just taken
along the two perpendicular directions defined by the polarizer. So, if the
incoming electric field vector, 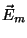 , makes an angle
, makes an angle 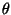 relative to the polarizing direction, we may
decompose that vector into its component along the polarizing direction, which
will have value
relative to the polarizing direction, we may
decompose that vector into its component along the polarizing direction, which
will have value 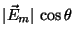 , and its component perpendicular to the
polarizing direction, which would then have value
, and its component perpendicular to the
polarizing direction, which would then have value 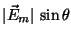 . This second portion would be absorbed so that
only the light along the polarizing direction would exit the material. The light
exiting this polarizer would then be plane polarized, and have less intensity
than when it entered since a portion of its energy had been absorbed. See the
Law of Malus in the text, which basically has two parts:
. This second portion would be absorbed so that
only the light along the polarizing direction would exit the material. The light
exiting this polarizer would then be plane polarized, and have less intensity
than when it entered since a portion of its energy had been absorbed. See the
Law of Malus in the text, which basically has two parts:
- if the incoming light is plane polarized, at angle
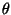 relative to the polarizing direction, then the
ratio of the intensity of the outgoing light to that of the incoming light is
given by
relative to the polarizing direction, then the
ratio of the intensity of the outgoing light to that of the incoming light is
given by 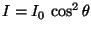 .
.
- if the incoming light is unpolarized, then we should treat it as a large,
random assembly of plane polarized incoming beams, which says we should
average over all possible angles. The average of
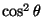 is one half, so that the final intensity is
given by
is one half, so that the final intensity is
given by 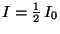 .
.
Birefringent materials
We could describe the previous process, namely the absorption of the one
component of the light while passing the other component directly through, as
changing the speed of the two components, so that one has speed zero and the
other has its speed unchanged. This causes us to consider rather more
sophisticated materials where the light is also split into two (or more)
components, and these two components pass through the material with different
speeds. These more general materials are referred to as birefringent, or
doubly refracting, materials. Typically such materials are crystals, so that
they can easily have a special direction within them, called the optic
axis, and light moving through this crystal which has its polarization
vector (or a component of that vector) along the optic axis moves with a
different speed than light with its polarization vector perpendicular to the
optic axis. To describe this, we must associate with the crystal two different
indices of refraction, no, the index for ``ordinary''
rays, and ne, the index for ``extraordinary" rays. (As
an amusing fact, it is sometimes true that extraordinary rays travel faster than
ordinary ones, as in calcite and dolomite, while in other materials the
extraordinary rays travel slower than the ordinary ones, as in quartz and ice.)
[It should also be pointed out that there are in the world trirefringent
materials, which need three different indices of refraction; topaz is an
example. However, we shall not discuss them here.] By allowing a light ray to be
incident on a birefringent material we may manipulate its polarization state. In
the general case the incoming light will have a polarization vector that has
non-zero components both along the optic axis and perpendicular to it. These two
components will then move through the crystal with two different speeds, at two
different directions--because Snell's Law for refraction depends on the
speed--and therefore through two different distances. In the general case this
will cause two different beams of light to exit the crystal where only one
entered; our standard example is a calcite crystal. Both those beams will of
course be plane polarized, whether or not the incoming light was polarized. A
somewhat special case, but a very interesting one and a common one, is obtained
when the crystal has its optic axis in one of its faces, i.e., in the plane of
its surface. (One could also cut the crystal to cause this if it didn't happen
naturally.) The scenario described above is still the valid one for an arbitrary
incoming light ray; however, if we now consider the special case of light
incident at zero angle on the surface, i.e, normally incident, then Snell's Law
will tell us that the light ray will go straight on through, i.e., the angle of
incidence is 0, so the angle of refraction is also 0, independent of the speed
of the wave inside the crystal. Therefore the two beams will exit at the same
place, and will be recombined into a single light ray again. However, since the
two beams required different times to make the transit through the crystal the
two beams being recombined--upon exit--will have begun their journey at
different times; i.e., they will be components of two different incoming waves,
and therefore will have different phases. By changing the thickness of the
crystal, we can manipulate this phase difference when the two are recombined. In
general crystals which have been cut this way are referred to as wave
plates. In the next section we will describe how this feature may be used to
create, for instance, circularly-polarized light from plane-polarized light, or
vice versa.
quarter-wave Plates and Circular Polarization
If the birefringent material is of thickness T, then the time required to
pass through it is simply t = T/v = n(T/c). Therefore if the two components have
indices of refraction no and
ne, the difference in time required for them to pass
through the crystal is 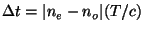 . To convert a time difference into a phase
difference, for the two components about to be combined, we multiply by the
angular frequency,
. To convert a time difference into a phase
difference, for the two components about to be combined, we multiply by the
angular frequency, 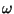 , which is the same for both waves:
, which is the same for both waves:
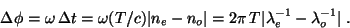 |
(3) |
We now suppose that our crystal has incoming, plane-polarized light ray
normally incident upon it. As well, label the direction of the optic axis by
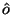 and the perpendicular direction in the crystal
surface by
and the perpendicular direction in the crystal
surface by 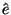 . Then the statement that the incoming
polarization direction is at an angle
. Then the statement that the incoming
polarization direction is at an angle 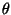 relative to the optic axis of the crystal allows
us to divide the incoming beam up into two components, as it enters the crystal,
at time t and at location x:
relative to the optic axis of the crystal allows
us to divide the incoming beam up into two components, as it enters the crystal,
at time t and at location x:
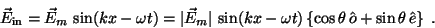 |
(4) |
Notice that the direction of the electric field is independent of time,
and that the portion inside the braces has magnitude 1. The intensity associated
with this electric field is the time-average of its square. Since the average
over a period of the square of a sine function is one half, the intensity is
proportional to 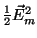 . When the light exits the crystal, having
travelled a distance T, the two components will be re-combined into a total
electric field vector again, being now at time t' and location x'. However, one
component has travelled longer than the other, and therefore has a different
phase, i.e., started earlier:
. When the light exits the crystal, having
travelled a distance T, the two components will be re-combined into a total
electric field vector again, being now at time t' and location x'. However, one
component has travelled longer than the other, and therefore has a different
phase, i.e., started earlier:
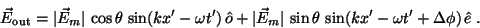 |
(5) |
In general this is quite a complicated-appearing equation, and gives us
light with some variety of elliptical polarization. However, in the following
special case we can use this phenomenon to create circularly-polarized light. We
must first require that the phase difference be one quarter of an entire cycle,
i.e., 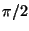 radians, or (of course) five quarters, or nine
quarters, etc. Secondly, we must require that the initial angle be 45 degrees.
Since the cosine of 45 degrees is the same as the sine, the magnitude of the two
components is therefore the same, and we have
radians, or (of course) five quarters, or nine
quarters, etc. Secondly, we must require that the initial angle be 45 degrees.
Since the cosine of 45 degrees is the same as the sine, the magnitude of the two
components is therefore the same, and we have
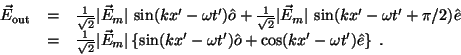 |
(6) |
The quantity in the braces is now rotating as time progresses, but always
has the same length, i.e., just 1. This is our requirement for circular
polarization! Moreover we notice that the time-average of the intensity is still
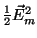 , the same as it was when it entered. We may
summarize by saying that if the phase difference of the two waves is one quarter
of an entire cycle, or an entire wavelength, then this crystal may be used to
create circularly-polarized waves from plane polarized ones. Therefore, they are
customarily referred to as quarter-wave plates. The thickness will of
course depend on the difference in the indices of refraction. We may determine
an explicit formula easily enough from our formula above for the phase
difference, which we now require to be
, the same as it was when it entered. We may
summarize by saying that if the phase difference of the two waves is one quarter
of an entire cycle, or an entire wavelength, then this crystal may be used to
create circularly-polarized waves from plane polarized ones. Therefore, they are
customarily referred to as quarter-wave plates. The thickness will of
course depend on the difference in the indices of refraction. We may determine
an explicit formula easily enough from our formula above for the phase
difference, which we now require to be 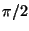 , where we also now look at the case when
, where we also now look at the case when 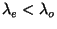 :
:
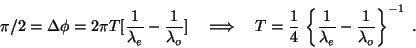 |
(7) |
We see that a quarter-wave plate satisfies that requirement for only one
particular wavelength, although ``nearby" wavelengths should not be too
different. However, if, for instance, we have a quarter-wave plate for violet
light, at 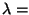 400 nm, then it would be a half-wave plate for
light at 800 nm, so that red light, being ``almost" that long, would have its
plane of polarization changed instead of becoming circularly polarized. To
better understand the last statement, let us retreat to Eq. (5) and consider the
case where the phase difference is half a wave, i.e.,
400 nm, then it would be a half-wave plate for
light at 800 nm, so that red light, being ``almost" that long, would have its
plane of polarization changed instead of becoming circularly polarized. To
better understand the last statement, let us retreat to Eq. (5) and consider the
case where the phase difference is half a wave, i.e.,  . In that case, again at an angle of 45 degrees,
the outgoing wave looks like
. In that case, again at an angle of 45 degrees,
the outgoing wave looks like
 |
(8) |
This time the quantity in the braces is again constant, and therefore
plane polarized. However, for our 45-degree incidence case, it entered as 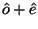 , and is now exiting as
, and is now exiting as 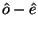 . These two directions are perpendicular to one
another, so that the plane of polarization is still constant, but has been
rotated by 90 degrees relative to its original direction.
. These two directions are perpendicular to one
another, so that the plane of polarization is still constant, but has been
rotated by 90 degrees relative to its original direction.
![next]()
![up]()
![previous]()
Next:
About this document ...
Daniel Finley
2001-01-23 ![]() , makes an angle
, makes an angle ![]() relative to the polarizing direction, we may
decompose that vector into its component along the polarizing direction, which
will have value
relative to the polarizing direction, we may
decompose that vector into its component along the polarizing direction, which
will have value ![]() , and its component perpendicular to the
polarizing direction, which would then have value
, and its component perpendicular to the
polarizing direction, which would then have value ![]() . This second portion would be absorbed so that
only the light along the polarizing direction would exit the material. The light
exiting this polarizer would then be plane polarized, and have less intensity
than when it entered since a portion of its energy had been absorbed. See the
Law of Malus in the text, which basically has two parts:
. This second portion would be absorbed so that
only the light along the polarizing direction would exit the material. The light
exiting this polarizer would then be plane polarized, and have less intensity
than when it entered since a portion of its energy had been absorbed. See the
Law of Malus in the text, which basically has two parts:
![]() . To convert a time difference into a phase
difference, for the two components about to be combined, we multiply by the
angular frequency,
. To convert a time difference into a phase
difference, for the two components about to be combined, we multiply by the
angular frequency, ![]() , which is the same for both waves:
, which is the same for both waves: