Reflection and Refraction of light

REFLECTION AND REFRACTION OF LIGHT (FRESNEL FORMULAS)

Let us consider the beam of light incident on the boundary surface between two substances - glass with refractive index n=1.5 and air with refractive index n=1. One part of light will reflect from such a boundary surface and other part will pass through it being refracted. The total energy in the reflected and refracted rays is equal to the energy of the incident light, but the proportion of the intensities in these two rays will depend upon the refractive index difference, the angle of incidence, the light polarization and direction in which the light is passing the border (from glass to air or from air to glass). Animations below show four possible cases of the light beam transmission:

	Glass -> Air	Video	Air -> Glass	Video
Parallel polarization
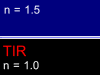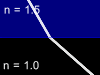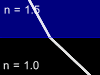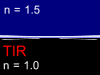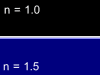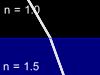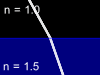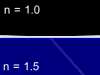Perpendicular polarization

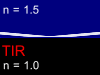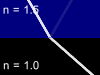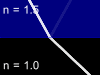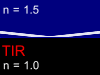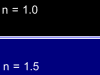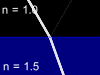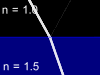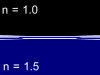The polarization is called parallel when the vector of electric field E lies in the plane of incident ray and normal to the border (see the figure below). In other case the polarization is called perpendicular

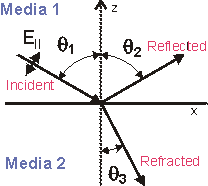Drawing of rays According to Fresnel formula the angles q₁of the incident wave, q₂ of the reflected wave and q₃ of the refracted wave are given by the equation:

q₁ = q₂

n₁sinq₁ = n₂sinq₃

The intensity reflection coefficients R_||and R_^ and transmission coefficients T_|| and T_^ (for the parallel and perpendicular polarization consequently) are described by the equations: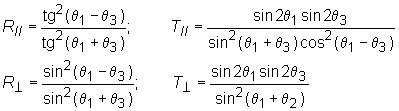

Fresnel formulas for reflection and transmission coefficients

For the ray incident normally to the border there is no difference between the parallel and perpendicular components. In this case we can write:

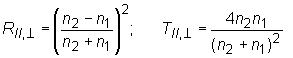
Fresnel formulas for the normally incident ray

The dependencies for the reflection coefficients R and for transmission coefficients T are given in the following figures:

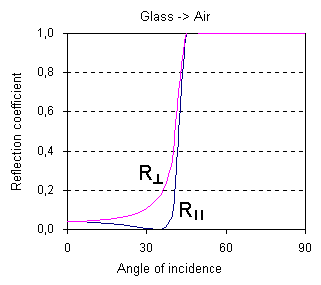Fresnel reflection coefficients for the boundary surface Glass->Air We can see from these figures and animations that for the light incident from the glass into the air there is an angle when the Total Internal Reflection (TIR) is observed. This means that any ray propagating in a glass at angles bigger than a critical angle (about 42° for glass-air interface) will be totally reflected and will not pass into the air. This effect is used for transmission of the light signals by the glass fiber over the large distance without a considerable attenuation.

q_TIR = arcsin(n₂/n₁), n₁ > n₂

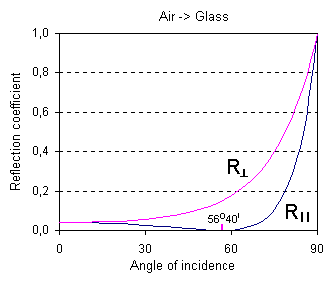Fresnel reflection coefficients for the boundary surface Air->Glass We can see also in the figure that for the light propagating from the air into the glass there is an angle at which the light with parallel polarization will not reflect, while the intensity of the perpendicularly polarized light is not zero. This angle is called Brewster's angle (56°40' for glass-air interface) and used for creation of the light polarizers and in lasers.

q_BR = arctg(n₂/n₁), n₁ < n₂